Estadística… Esa ciencia que dice que si tu te comiste un pollo y yo no comí nada, cada uno de los dos nos comimos medio pollo. Tan falsa y tan cierta, tan inútil y tan necesaria. Todo depende de quién la use y para qué. Desde un científico que necesita analizar la veracidad de sus resultados, hasta un político que busca un argumento convincente para su propuesta, sea cierto o no.
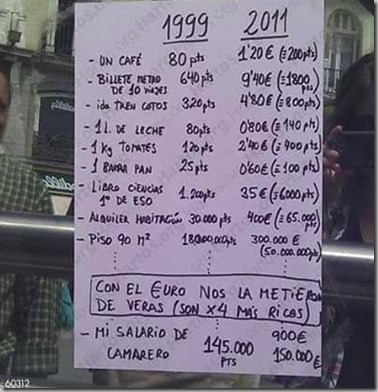
Un ejemplo: últimamente se ha hecho viral esta foto:
En ese papel se comparan precios de 1999 y 2011, y afirma que son 4 veces más caros. Lo cierto es que si uno hace el cálculo, el incremento no es de 4 veces más sino “solo” 2.5 veces más. Pero da igual… es bastante cierto todo lo que pone, y un incremento de 2.5x sigue siendo un escándalo. Así que si, ¡oye! tiene su punto. Y cuando uno lo lee, y repasa mentalmente los precios que recuerda de aquellos años, enseguida dice: “¡tiene más razón que un santo!, con el Euro, efectivamente nos la han metido doblada”. Bueno, puede que sí, y puede que no…
La gente no suele pararse a pensar en un “error” básico que se comete casi siempre: utilizar un conjunto de muestras demasiado pequeño y desviado. En otras palabras: de los miles y miles de productos que consumimos, ahí solo menciona 8 o 9.
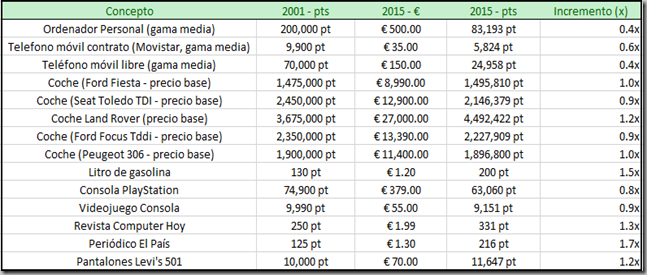
Es evidente que la validez de una estadística depende del conjunto de muestras utilizadas, y de lo bien (o mal) que representa a la población general. Pongamos otro ejemplo: me he tomado unos minutos para buscar anuncios en Youtube de los años 1999-2001, para poder comparar otros precios con los actuales, y he obtenido estos resultados:
Si calculáis la media del incremento (o decremento) de precios en esos casos, ¿sabéis que sale?
1.0x
Es decir, según esa tabla, los precios no han subido absolutamente nada en los últimos 15 años, algo que sabemos es rotundamente falso.
Si ahora combinamos ambas tablas, extendiendo el espacio de muestras para que incluya todos los productos, obtenemos lo siguiente:
Si de nuevo calculamos la media del incremento de precios, esta vez obtenemos: 1.6x. Bastante alejado del 1.0x, pero más aún del 4x que mencionaba el papel de la foto.
Es evidente que la fiabilidad y precisión de una estadística va creciendo conforme se aumenta el espacio de muestras. El problema es: ¿a partir de qué punto se considera que el espacio de muestras representa con suficiente fiabilidad al conjunto de la población? La estadística ofrece herramientas para medir estas desviaciones, pero el problema es que nadie las utiliza. Más aún, cuando se ofrece una estadística, ni siquiera nos informan de cómo era el espacio de muestras…
Otro ejemplo: las predecibles encuestas de determinados canales de Tv, que siempre obtienen resultados que se alinean con su ideología:
Lo que no nos dicen es que quizá en esa encuesta hayan votado 14 personas (que ya de por sí están sesgadas por el mero hecho de ver ese canal). Es otro ejemplo de un espacio de muestras ridículamente sesgado, cuyos resultados no sirven para nada (más allá de para intentar manipular).
El problema es que estamos tan acostumbrados a esto, que ni siquiera nos preocupamos de informarnos como es debido. Cuando oímos una estadística, el único filtro por el que la pasamos es nuestra propia ideología: si es algo que se alinea con nuestra forma de ver la vida, nos lo creemos sin vacilar. Si no, simplemente lo ignoramos o (entonces sí) decidimos que probablemente ese periodicucho es parcial o partidista.
Así que si… somos extremadamente fáciles de manipular. Y esto lo hacen absolutamente todos los medios y partidos. De derecha, de izquierda, de centro y de dentro…
De igual forma que los alimentos deben incluir información nutricional, o los medicamentos informar sobre sus efectos secundarios, deberíamos exigir que los medios, los políticos, todo el mundo… estuvieran obligados a informar sobre el tamaño y la representatividad de las muestras que ha utilizado al obtener una estadística.
Así, la próxima vez que nos la intenten colar algo como “no se qué problema está mejorando (o empeorando)” y tengan que reconocer que solo han preguntado a 200 personas, no solo sabremos que no debemos hacer caso a ese dato, sino que la persona en cuestión quedará en ridículo y en el futuro se verá obligada a realizar estadísticas más realistas.
He hecho una encuesta en mi oficina, y el 85% de la gente está de acuerdo conmigo en esto…